

Basic GLM and Logistic Regression
Adam J Sullivan
Assistant Professor of Biostatistics
Brown University
Generalized Linear Models
Generalized Linear Models
- We will introduce a topic that is typically taught only in a class where you are expected to know linear algebra.
- Fear not though!
- We will show some of the math behind this but this is to teach you methods that link to the modern way data analysis is done.
Why Bother?
- By learning the Generalized Linear Models we can understand how to fit, linear, logistic, Poisson, multinomial, data from distributions like Gamma and Inverse Gamma, longitudinal data and multivariate data.
- We will not have time to learn all of these in this class but this is a very versatile model.
- The mathematics behind these models are matrix related but we will focus on the application of them.
The Generalized Linear Model
- The generalized linear model refers to a whole family of models.
- They became popular with a book by McCullagh and Nelder (1982).
- They have 3 basic components.
Components of any GLM
- The Random Component - probability distribution of the response variable. In linear regression this is the normal distribution.
- The Systematic Component - fixed structure of explanatory variables usually a linear function. We have seen this as \(\beta_0 + \beta_1X_1 + \ldots\).
- The Link Function - maps the systematic component onto the random component. This was \(E(Y_i|X_{1i}, \ldots)\) in the linear regression case.
The Random Component
- Observations of the outcome represent a sample from a random variable.
- This random variable has a mean value and variation that depends on the distribution it follows.
- GLM uses random variables that follow an exponential family distribution.
The Systematic Component
- We use the covariates or independent variables to model to estimate the means of the random variable that our sample was drawn from.
- This is added to the variation to give use the data that we observed.
The Model
We use \[\eta_i = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \cdots + \beta_px_{ip} = \sum_{j=1}^p \beta_jx_{ij}\]
where:
- \(\eta\) is the linear predictor.
- \(x_1, \ldots, x_p\) are the explanatory variables.
- \(\beta_1,\ldots,\beta_p\) are the coefficients of the explanatory variables.
- \(\beta_0\) is the value of \(\eta\) when all the \(x\)'s are 0.
What you typically will see:
- Most of the time this is written as: \[\mathbf{\eta} = \mathbf{X\beta} \]
- where:
- \(\mathbf{\eta}=(\eta_1, \ldots, \eta_N)^T\) is a column vector.
- \(\mathbf{\beta} = (\beta_0, \ldots,\beta_p)^T\) is a column vector.
- \(\mathbf{X}\) is a \(N\times p\) matrix of the explanatory variables \(x_{ij}\) for \(i=1,\ldots,N\) and \(j=1,\ldots,p\).
Visualizing the Matrices
- In other words: \[\mathbf{\eta}= \left[\begin{array}{c} \eta_1 \\ \vdots \\ \eta_N \end{array} \right]= \left[\begin{array}{cccc} 1& x_{11} & \ldots & x_{1p} \\ 1& x_{21} & \ldots & x_{2p} \\ \vdots& \vdots & \vdots & \vdots\\ 1& x_{N1} & \ldots & x_{Np} \end{array}\right]\left[\begin{array}{c} \beta_0\\ \beta_1 \\ \vdots\\ \beta_p \end{array}\right]= \mathbf{X}\mathbf{\beta}\]
- This linear predictor allows the least squares regression approach to be generalized to a wide range of models.
The Link Function
- We cannot always model a direct relationship between the random and the systematic component.
- This is where the link function comes into place.
- This function allows us to specify a relationship between the linear(systematic component) and the random component.
- We essentially link \(\eta_i\) to \(\mu_i=E(y_i)\).
The Link Function
- We have \[g(\mu_i) = \eta_i\]
- where:
- \(g()\) is the link function.
- \(\mu_i\) represents the expected value of the random component.
- \(\eta_i\) represents the linear(structural) component.
What is this link Function?
- The link function is specifically defined by how the distribution is identified as an exponential family.
- We will not go through this math however feel free to look up exponential families and try and put the distributions we talk about into this framework.
Common Link Functions:
Some common link functions are
Random Component Link Function Outcome Explanatory Model Normal Identity Continuous Factor ANOVA Normal Identity Continuous Continuous Regression Binomial Logit Binary Mixed Logistic Regression Multinomial Generalized logit Binary Mixed Multinomial Regression Poisson Log Count Mixed Poisson Regression
What Does this Mean?
- The chart shows just some of the many types of models we can learn to do just from a simple concept of GLMs.
- Essentially every type of technique you have used up until this point can be structured in such a way that is represents a GLM.
Assumptions of a GLM
- The data \(Y_1, Y_2, \ldots, Y_2\) are independently distributed.
- The dependent variable \(Y_i\) is from an exponential family.
- Normal (Gaussian)
- Bernoulli
- Binomial
- Multinomial
- Exponential
- Poisson
Assumptions of a GLM
- Linear Relationship between link function and systematic component.
- Errors are independent.
What Assumptions are not needed?
- We do NOT some assumptions we needed before.
- We do NOT need a linear relationship between the dependent variable and the independent variables.
- We do NOT need need normally distributed errors.
- We do NOT need homogeneity of errors.
What Elses is Different?
- Uses Maximum Likelihood Estimation rather than Least Squares Estimation.
- For goodness-of-fit tests need large sample sizes. (Rule of thumb not more than 20\% of cell counts in tables are less than 5).
The Case of Linear Regression
Linear Regression as a Case
- We have previously been using linear regression and it can be easily display how we use it in this framework.
- For example in a multiple linear regression we have \[y_i|x_{i1},\ldots,x_{ip} = \beta_0 + \beta_1x_{i1} + \cdots + \beta_px_{ip} + \epsilon_i\]
- Then we know that \[\mu_i = E(y_iy_i|x_{i1},\ldots,x_{ip}) = \beta_0 + \beta_1x_{i1} + \cdots + \beta_px_{ip}\]
- Thus we can directly relate \(\mu_i\) to the systematic component.
What Link in the Linear Case?
- Thus in this case our function \(g()\) is \[g(\mu_i) = \mu_i\]
- We call this the identity link.
What do we have?
- Then we have that
- Random Component: \(y\) is the outcome and is normally distributed. So we let \(\epsilon_i\sim N(0\sigma^2)\).
- Systematic Component: \(x_1,\ldots,x_p\) are the explanatory variables. They can be categorical or continuous. We have a linear combination of these terms but we can still have \(x^2\) or \(\log(x)\) terms in here as well.
- Link Function:
Identity Link
- We have the identity function: \[ \begin{aligned} \eta &= \beta_0 + \beta_1x_{i1} + \cdots + \beta_px_{ip} \\ g(E(y_i)) &= \beta_0 + \beta_1x_{i1} + \cdots + \beta_px_{ip} \\ g(E(y_i)) &= E(y_i) \end{aligned} \]
- With linear regression we have the simplest link function because we are able to model the mean directly.
The Case of Logistic Regression
Logistic Regression
- We will now move onto logistic regression.
- With logistic regression we are concerned with binary data.
- This is data that is in a format of either yes or no, 0 or 1, or some variation of that.
Binomial Distribution
- If we consider binary data we find that what we have is called the Binomial distribution.
- Let's assume that we have \(Y\) where
\[ Y = \begin{cases} 1 & \text{if sucess}\\ 0 & \text{if failure} \end{cases} \]
What Does this mean?
- Then \[\Pr(Y=y) =\binom{n}{y} p^y(1-p)^{n-y} \]
- where \(p\) is the probability that \(Y=1\).
- This leads us to
\[E(Y) = np\] \[Var(Y)= np(1-p)\]
Regression Model for Logistic
- Recall from simple linear regression that our systematic part of our model is \[E(Y_i|x_i) = \beta_0 + \beta_1x_i\]
- That would mean with this type of data we have \[p_i = \beta_0 + \beta_1 x_i\]
Why Can't we do Linear Regresion?
- The issue with this is now we can have values that fall outside of 0 and 1.
- To overcome the problem with negative values we could exponeniate: \[p_i = \exp\left(\beta_0 + \beta_1x_1\right)\]
- We now have values that can fall between 0 and infinity.
What about Values greater than 1?
- In order to solve the problem of values being greater than 1, we divide by 1 plus the exponential: \[p_i= \dfrac{\exp\left(\beta_0 + \beta_1x\right)}{1+\exp\left(\beta_0 + \beta_1x_1\right)}\]
- This new function now lies completely between 0 and 1 as needed.
- Then we solve back to where we have the systematic part.
The Systematic Part
\[ \begin{aligned} p_i &= \dfrac{\exp\left(\beta_0 + \beta_1x_i\right)}{1+\exp\left(\beta_0 + \beta_1x_i\right)}\\ p_i\left(1+\exp\left(\beta_0 + \beta_1x_i\right)\right)&=\exp\left(\beta_0 + \beta_1x_i\right)\\ p_i &= \exp\left(\beta_0 + \beta_1x_i\right)\left(1-p_i\right)\\ \log\left(\dfrac{p_i}{1-p_i}\right) &= \beta_0 + \beta_1x_i\\ logit\left(p_i\right) &= \beta_0 + \beta_1x_i \end{aligned} \]
What does this mean?
- This means we are fitting a linear regression to the logistic unit (logit) or the log odds of the probability of a success.
- This is why we refer to this as logistic regression.
The Logit
Then if we consider the logit:
\[ \begin{aligned} \text{If } p= 0 & \text{then } \log\left(\dfrac{p}{1-p}\right)=-\infty\\ \text{If } p= \tfrac{1}{2} & \text{then } \log\left(\dfrac{p}{1-p}\right)=0\\ \text{If } p= 1 & \text{then } \log\left(\dfrac{p}{1-p}\right)=\infty \end{aligned} \]
What does the Logit imply?
- We can see that as \(p\) increases the logit does as well.
- We have that the logit can be anything between \(-\infty\) and \(\infty\), but \(p\) is between 0 and 1 as needed.
Relationship Between \(p\) and the logit
- We can see the relationship between \(p\) and the logit below.
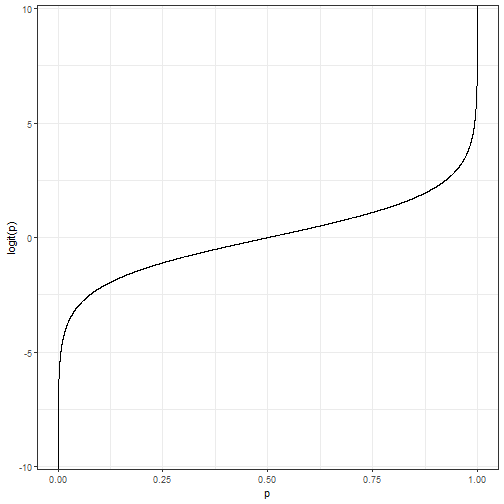
Logistic as a GLM
- From the above work we can see that with logistic regression we have \[log\left(\dfrac{p}{1-p}\right) = \beta_0 + \beta_1x_1\] \[\text{or}\] \[log\left(\dfrac{p}{1-p}\right) = \beta_0 + \beta_1x_1 + \cdots + \beta_px_p\]
Logistic as a GLM
- Where \(E(y_i|y_{i1},\ldots, x_{ip}) = p_i\) therefore what we have is
- Random Component: \(y\) is the outcome and is binomial and we assume the variance to be that of a binomial.
- Systematic Component: \(x_1,\ldots,x_p\) are the explanatory variables. They can be categorical or continuous.
- We have a linear combination of these terms but we can still have \(x^2\) or \(\log(x)\) terms in here as well.
The Link Funcion:
- Where \(E(y_i|y_{i1},\ldots, x_{ip}) = p_i\) therefore what we have is
- Link Function: We can see from above that with \(p_i\) being the mean that we have the logit as the link function:
\[ \begin{aligned} \eta &= \beta_0 + \beta_1x_{i1} + \cdots + \beta_px_{ip} \\ g(E(y_i)) &= \beta_0 + \beta_1x_{i1} + \cdots + \beta_px_{ip} \\ g(p_i) &= logit\left(p_i\right) \end{aligned} \]
Maximum Likelihood Estimation
- In linear regression we learned about least squares estimation.
- This falls apart with logistic regression when we have \(p=0\) or \(p=1\).
- Due to this we prefer a technique that can accurately estimate \(p\) no matter what.
- We will map out what this looks like right now.
Our Data
- With our data we have \[\Pr(Y_i=1|x_i) = \dfrac{\exp\left(\beta_0 + \beta_1x_i\right)}{1+ \exp\left(\beta_0+\beta_1x_i\right)}\]
- Then we also have that
\[ \begin{aligned} \Pr(Y_i=0|x_i) &= 1- \Pr(Y_i=1|x_i)\\ &= 1 - \dfrac{\exp\left(\beta_0 + \beta_1x_i\right)}{1+ \exp\left(\beta_0+\beta_1x_i\right)}\\ &= \dfrac{1}{1+ \exp\left(\beta_0+\beta_1x_i\right)} \end{aligned} \]
Our Data
- If we combine these together we find that: \[\Pr(Y_i=y_i|x_i) = \dfrac{\exp\left(\left(\beta_0 + \beta_1x_i\right)\cdot y_i\right)}{1+ \exp\left(\beta_0+\beta_1x_i\right)}, \;\;\;y_i=0,1\]
The Likelihood
- The likelihood is defined as the probability of obtaining the data that was observed. \[\Pr(Y_1=y_1, Y_2=y_2, \ldots, Y_n=y_n| x_1,x_2,\ldots,x_n)\]
- Then we assumed that in our data the responses are independent from one another.
- This leads to \[\Pr(Y_1=y_1, Y_2=y_2, \ldots, Y_n=y_n| x_1,x_2,\ldots,x_n) = \Pr(Y_1=y_1|x_1)\cdots \Pr(Y_n=y_n|x_n)\]
The Likelihood
- Then the probability we obtain our data is \[L = \prod_{i=1}^n \left[ \dfrac{\exp\left(\left(\beta_0 + \beta_1x_i\right)\cdot y_i\right)}{1+ \exp\left(\beta_0+\beta_1x_i\right)}\right]\]
Maximum Likelihood
- Maximum likelihood estimates for \(\beta_0\) and \(\beta_1\) are found by searching for which values \(\hat{\beta}_0\) and \(\hat{\beta}_1\) maximize \(L\).
- Unlike in least squares we cannot find these solutions in a closed form.
- We calculate MLEs with some sort of iterative technique.
Normal Distribution and Maximum Likelihood
- It can be shown that maximum likelihood estimators are normally distributed.
- This means in our data \[\hat{\beta}_0 \stackrel{approx}{\sim} N\left(\beta_0, \widehat{Var}\left(\hat{\beta_0}\right)\right)\] \[\hat{\beta}_1 \stackrel{approx}{\sim} N\left(\beta_1, \widehat{Var}\left(\hat{\beta_1}\right)\right)\]
Why do we use MLE?
- Finally we have that MLEs are the most efficient estimators out there.
- Meaning that any other consistent estimators \(\tilde{\beta}_0\) and \(\tilde{\beta}_1\) will have larger variances then \(\hat{\beta}_0\) and \(\hat{\beta}_1\).
- This means we will have the tightest confidence intervals around our MLEs and possibly show significance when other estimators would fail to.
Simple Logistic Regression
Simple Logistic Regression
- We will begin with an example of simple logistic regression with a sample of the Western Collaborative Group Study.
- This study began in 1960 with 3154 men ages 39-59, who were employed in one of 11 California based companies.
- They were followed until 1969 during this time, 257 of these men developed coronary heart disease (CHD).
- You can read this data in with the code below.
Reading in the Data
library(haven)
wcgs <- read_dta("wcgs2.dta")
wcgs <- wcgs[,-16]
The Variables
| Name | Description |
|---|---|
| id | Subject identification number |
| age | Age in years |
| height | Height in inches |
| weight | Weight in lbs. |
| sbp | Systolic blood pressure in mm |
| dbp | Diastolic blood pressure in mm Hg |
| chol | Fasting serum cholesterol in mm |
The Variables
| Name | Description |
|---|---|
| behpat | Behavior |
| 1 = A1 | |
| 2 = A2 | |
| 3 = B3 | |
| 4 = B4 | |
| ncigs | Cigarettes per day |
| dibpat | Behavior |
| 1 = type A | |
| 2 = type B |
The Variables
| Name | Description |
|---|---|
| chd69 | Coronary heart disease |
| 1 = Yes | |
| 0 = no | |
| typechd | Type of CHD |
| 1 = myocardial infarction or death | |
| 2 = silent myocardial infarction | |
| 3 = angina perctoris | |
| time169 | Time of CHD event or end of follow-up |
The Variables
| Name | Description |
|---|---|
| arcus | Arcus senilis |
| 0 = absent | |
| 1 = present | |
| bmi | Body Mass Index |
Continuous Covariate
- We will first consider the relationship between age and CHD.
- We could first consider boxplots
What do we see?
- This displays that the group with CHD appears older than the group without a CHD.
- To check if there is an increased probability of CHD due to being older we will fit the following logistic regression. \[logit(p_{CHD}) = \hat{\beta}_0 + \hat{\beta}_1 Age\]
What do We See?
library(broom)
fit.cont <- glm(chd69 ~ age, data=wcgs, family=binomial(link="logit"))
tidy(fit.cont, conf.int=TRUE)[,-c(3:4)]
## # A tibble: 2 x 5
## term estimate p.value conf.low conf.high
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) -5.94 3.00e-27 -7.02 -4.87
## 2 age 0.0744 4.56e-11 0.0523 0.0966
What can we conclude?
- From here he can reject the null hypothesis and conclude that \(\beta\ne0\) and further more show that the probability of having CHD increases with age.