• For binary data we have used the binomial distribution and logistic regression.
• For count data we have used the Poisson distribution and Poisson/Log-linear regression.
• Survival data is positive and usually continuous

For this reason we use continuous distributions but ones other than normal. We will discuss a couple of these:

1. The exponential Distribution
2. The Weibull Distribution

This is the simplest situation

• Assumption of Constant hazard
• This may work over short time periods but is unlikely in the long run.
• Survival analysis with the exponential distribution is equivalent to Poisson Regression.

We have a random variable \(T\) which is the failure time

• Hazard Function: \(h(t)=\lambda\)
• Survivor Function: \(S(t) = e^{-\lambda t}\)
• Median: \(T_{med} = \dfrac{\log(2)}{\lambda}\)
• Mean: \(E(T) = \dfrac{1}{\lambda}\)

If treatment cuts the hazard in half, the median survival time is doubled

• If survival times follow an exponential distribution with the hazard \(\lambda\) then the number of events \(t\) follows a Poisson distribution with mortality rate \(\lambda\).

• Thus when we use Poisson regression the estimated regression coefficients are interpreted as log-hazard ratios.

For example:

Let

• \(X=1\) for subjects with diabetes
• \(X=0\) for subjects without diabetes

Then the exponential regression model is

\[h(t|X=x) = \exp(\beta_0+\beta_1x) = \exp(\beta_0)\exp(\beta_1x)\] This means

\[\begin{aligned} \log\left[h(t|X=0)\right] &= \beta_0\\ &= \log\left( \text{ hazard among people without diabetes}\right)\\ \log\left[h(t|X=1)\right] &= \beta_0 + \beta_1\\ &= \log\left( \text{ hazard among people with diabetes}\right)\\ \beta_1 &= \log\left[h(t|X=1)\right]- \log\left[h(t|X=0)\right]\\ &= \dfrac{\log\left[h(t|X=1)\right]}{\log\left[h(t|X=0)\right]}\\ &= \log\left(\text{ hazard ratio, diabetes vs no diabetes}\right)\\ \end{aligned}\]

We typically test this assumption with a graph

• The cumulative hazard function for exponential is given by

\[\Lambda(t) = \int_0^th(u)du=\lambda t\] This implies that it is a straight line with slope \(\lambda\) and intercept 0.

• We can then use the Nelson-Aalen estimator which gives a non parametric estimation of cumulative hazard.
• If the model is exponential we can fit a straight line through this data.

• Assumption of constant hazard is not realistic
• The hazard may be higher after an intervention then decrease after a certain time.
• In healthy populations the hazards for most outcomes increase with age.
• The aging process by nature has an increasing hazard of death.

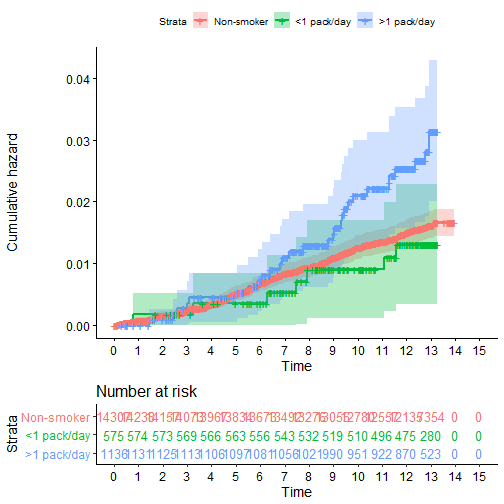
Recall our Colorectal Cancer data and smoking:

suppressMessages(library(foreign))
phscrc <- read.dta("https://drive.google.com/uc?export=download&id=0B8CsRLdwqzbzSno1bFF4SUpVQWs")
crc.haz <- survfit(Surv(cayrs, crc) ~ csmok, data= phscrc, type='fleming') 

suppressMessages(library(survminer))
ggsurvplot(crc.haz, conf.int = TRUE,
           risk.table = TRUE, risk.table.col = "strata",
           fun = "cumhaz", legend.labs = c("Non-smoker", "<1 pack/day", ">1 pack/day"),
          break.time.by=1)

We use the Weibull many times as an alternative to the exponential

The weibull has

• \(h(t) = \lambda\left(\gamma t^{\gamma-1}\right)\)
• \(\Lambda(t) = \lambda t^{\gamma}\)
• \(S(t) = e^{-\lambda t^\gamma}\)
• Then
  • If \(\gamma=1\) we have the exponential
  • If \(\gamma>1\) the hazard increases over time.
  • If \(\gamma<1\) the hazard decreases over time.

The model for weibull hazard is

\[h(t|X_1,\ldots,X_p ) = \lambda\gamma t ^{\gamma-1}\exp\left(\beta_0+\beta_1x_1+\cdots\beta_px_p\right)\]

Then

• baseline hazard is \(\lambda\gamma t ^{\gamma-1}\) and depends on \(t\)
• Covariates have a multiplicative effect on baseline hazard
  • hazards for 2 covariate levels are proportional
• Can be fit in R using survreg()

Weibull is not always applicable in some settings. For example

• If hazard increases of time (\(\lambda>1\)) then hazard is 0 at time \(t=0\)
• If hazard decreases of time (\(\lambda<1\)) then hazard is \(\infty\) at time \(t=0\)

• If the model for \(T\) is correct that we gain power with parametric models over KM and logrank.
• If the model for \(T\) is incorrect, parametric methods will be biased and non-parametric models will not be
• It is easier to control for confounding and to detect effect modification with parametric modeling.

For a time to event \(T\) and covariates \(X_1, \ldots , X_p\) the exponential regression model is:

\[h(t|X_1,\ldots, X_p) = \exp\left(\beta_0 + \beta_1x_1 + \cdots + \beta_px_p\right)\]

The baseline hazard function is defined as the hazard function when all covariates are 0

\[h(t|X_1=0,\ldots, X_p=0) = \exp\left(\beta_0 \right) = h_0(t) = h_0\]

Thus we can rewrite the model as: \[h(t|X_1,\ldots, X_p) = h_0\exp\left( \beta_1x_1 + \cdots + \beta_px_p\right)\]

This suggest that covariate effects are **multiplicative* on the constant baseline hazard, \(h_0\).

For a time to event \(T\) and covariates \(X_1, \ldots , X_p\) the Weibull regression model is:

\[h(t|X_1,\ldots, X_p) = \gamma t^{\gamma-1}\exp\left(\beta_0 + \beta_1x_1 + \cdots + \beta_px_p\right)\] with baseline hazard \[h_0(t) = \exp(\beta_0)\gamma t^{\gamma-1} = \lambda\gamma t^{\gamma-1}\] We can rewrite this as \[h(t|X_1,\ldots, X_p) = h_0(t)\exp\left(\beta_1x_1 + \cdots + \beta_px_p\right)\]

The general Proportional Hazards Model is \[h(t|X_1,\ldots, X_p) = h_0(t)\exp\left(\beta_1x_1 + \cdots + \beta_px_p\right)\]

\[\text{or}\]

\[\log\left[h(t|X_1,\ldots, X_p)\right] = \log\left[h_0(t)\right] + \beta_1x_1 + \cdots + \beta_px_p\]

where \(h_0(t)\) is the baseline hazard function and the "intercept" is \(\log\left[h_0(t)\right]\).

• Weibull and Exponential are examples of parametric proportional hazards models, where \(h_0(t)\) is a specified function.
• In 1972, Cox generalized these types of models so that we can make inferences on the \(\beta_1, \ldots,\beta_p\) without specifying \(h_0(t)\).
• We call Cox a semi-parametric regression model
• We fit this using something called Partial Likelihood Estimation
• Once again we use an algorithm to maximize the partial likelihood.

Let

• \(X=0\) be the control group
• \(X=1\) be the treatment group

Then

\[\begin{aligned} h(t|X=x) &= h_0(t)\exp(\beta x)\\ h(t|X=0) &= h_0(t)\\ &= \text{ baseline hazard for control group}\\ h(t|X=1) &= h_0(t)\exp(\beta)\\ &= \text{ hazard for treated group}\\ \exp(\beta) &= \dfrac{h(t|X=1)}{h(t|X=0)}\\ \end{aligned}\]

• This means that the hazard ratio is constant over time (Proportional Hazards)
• \(\beta\) is the log hazard ratio or log-relative risk
• According to the Cox model

\[\begin{aligned} \log\left[h]h(t|X=0)\right] &= \log\left[h_0(t)\right]\\ \log\left[h]h(t|X=1)\right] &= \log\left[h_0(t)\right] + \beta\\ \end{aligned}\]

• This means the log of the hazard functions are parallel over time.
• We make no assumptions about \(h_0(t)\).

Recall \[S(t) = \exp\left(-\Lambda(t)\right)\] with a binary \(X\) we have that

\[\begin{aligned} \Lambda_1(t) &= \Lambda_0(t)\exp(\beta)\\ S_0(t) &= \exp(\Lambda_0(t))\\ -\log(S_0(t)) &= \Lambda_0(t)\\ \log(-\log(S_0(t))) &=\log(\Lambda_0(t))\\ \end{aligned}\]

\[ \begin{aligned} S_1(t) = exp(-\Lambda_1(t)) &= \exp\left[\Lambda_0(t)\exp(\beta)\right]\\ -\log(S_1(t)) &= \Lambda_0(t)\exp(\beta)\\ \log(-\log(S_1(t))) &= \log(\Lambda_0(t)) + \beta\\ \end{aligned} \]

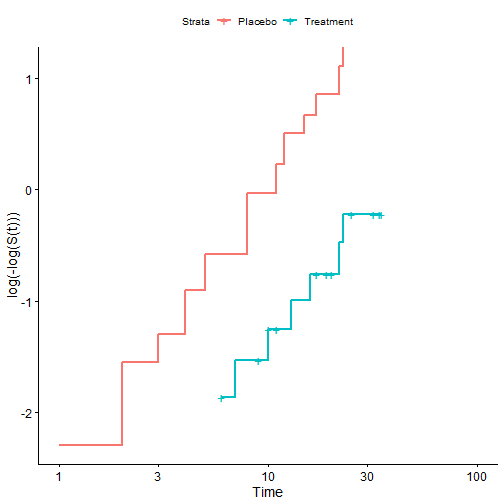
Thus we can see that under the assumption of proportional hazards

• \(\log(-\log(K-M))\) should be parallel over time.
• We typically verify this graphically.
• Recall the Leukemia study:

ggsurvplot(leukemia.surv,      
      legend.labs = c("Placebo", "Treatment"),break.time.by=5, 
            fun="cloglog")  

cox.leukemia <- coxph(Surv(T.all, event.all) ~ group.all , data=leuk2 )
summary(cox.leukemia)

## Call:
## coxph(formula = Surv(T.all, event.all) ~ group.all, data = leuk2)
## 
##   n= 42, number of events= 30 
## 
##             coef exp(coef) se(coef)     z Pr(>|z|)    
## group.all -1.572     0.208    0.412 -3.81  0.00014 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##           exp(coef) exp(-coef) lower .95 upper .95
## group.all     0.208       4.82    0.0925     0.466
## 
## Concordance= 0.69  (se = 0.041 )
## Rsquare= 0.322   (max possible= 0.988 )
## Likelihood ratio test= 16.4  on 1 df,   p=0.00005
## Wald test            = 14.5  on 1 df,   p=0.0001
## Score (logrank) test = 17.2  on 1 df,   p=0.00003

This would suggest that the hazard for those in a placebo group is 4.8 times that of those in the treated group.

For another example could look at Colorectal Cancer in the PHS:

crc.cox <- coxph(Surv(cayrs, crc) ~ csmok + age , data= phscrc)
summary(crc.cox)

Then we could say that for two people with the same smoking status a one year increase in age would lead to an 8.2% increase in the hazard of colorectal cancer with a 95% CI of 6.9% to 9.6%.

## Call:
## coxph(formula = Surv(cayrs, crc) ~ csmok + age, data = phscrc)
## 
##   n= 16018, number of events= 254 
##    (16 observations deleted due to missingness)
## 
##          coef exp(coef) se(coef)     z Pr(>|z|)    
## csmok 0.31715   1.37320  0.09767  3.25   0.0012 ** 
## age   0.07904   1.08224  0.00628 12.58   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
##       exp(coef) exp(-coef) lower .95 upper .95
## csmok      1.37      0.728      1.13      1.66
## age        1.08      0.924      1.07      1.10
## 
## Concordance= 0.724  (se = 0.015 )
## Rsquare= 0.01   (max possible= 0.262 )
## Likelihood ratio test= 160  on 2 df,   p=<2e-16
## Wald test            = 163  on 2 df,   p=<2e-16
## Score (logrank) test = 177  on 2 df,   p=<2e-16

library(SurvRegCensCov)
crc.exp <- survreg(Surv(cayrs, crc) ~ csmok + age, data= phscrc, dist='weibull')
ConvertWeibull(crc.exp)

## $vars
##          Estimate         SE
## lambda 0.00000664 0.00000295
## gamma  1.30451991 0.07929445
## csmok  0.31804318 0.09766224
## age    0.07916154 0.00627915
## 
## $HR
##         HR   LB   UB
## csmok 1.37 1.13 1.66
## age   1.08 1.07 1.10
## 
## $ETR
##         ETR    LB    UB
## csmok 0.784 0.675 0.910
## age   0.941 0.930 0.952