• Very popular tool in modern statistics.
• Involvees drawing samples from data and calculating statistics in the sample.
• Quick Example: Getting standard error and confidence intervals for non-normal data in linear regression

• SO far we have been using the validation or hold-out approach to estimate the prediction error of our predictive models.
• This involves randomly dividing the available set of observations into two parts, a training set and a testing set (aka validation set).
• Our statistical model is fit on the training set, and the fitted model is used to predict the responses for the observations in the validation set.

• The resulting validation set error rate (typically assessed using MSE in the case of a quantitative response) provides an estimate of the test error rate.
  
• The validation set approach is conceptually simple and is easy to implement. But it has two potential drawbacks:

• Bootstrapping is a widely applicable and extremely powerful statistical tool that can be used to quantify the uncertainty associated with a given estimator or statistical learning method.
• As a simple example, bootstraping can be used to estimate the standard errors of the coefficients from a linear regression fit.
• This may not seem necessary because we already achieve these through R, but bootstrapping may yield better standard errors.

• Other statistical methods are not as simple to get errors from.
• Bootstrapping can be a great way to understand variability.

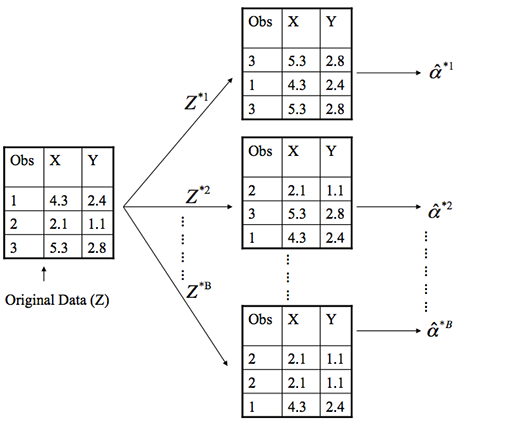
• Basically, bootstrapping treats the data as a population.
• The we repeatedly draw independent samples to create bootstrapped datasets.
• We sample with replacement, allowing observations to be sampled more than once.

• Each bootstrap data set \[Z^{*1}, Z^{*2}, \dots, Z^{*B}\] contains n observations, sampled with replacement from the original data set.
  
• Each bootstrap is used to compute the estimated statistic we are interested in \(\hat\alpha^*\).

• We can then use all the bootstrapped data sets to compute the standard error of \[\hat\alpha^{*1}, \hat\alpha^{*2}, \dots, \hat\alpha^{*B}\] desired statistic as \[ SE_B(\hat\alpha) = \sqrt{\frac{1}{B-1}\sum^B_{r=1}\bigg(\hat\alpha^{*r}-\frac{1}{B}\sum^B_{r'=1}\hat\alpha^{*r'}\bigg)^2} \tag{4} \]
• \[SE_B(\hat\alpha)\] serves as an estimate of the standard error of \[\hat\alpha\] estimated from the original data set.

• Performing a bootstrap analysis in R entails two steps:
  1. Create a function that computes the statistic of interest.
  2. Use the boot function from the boot package to perform the boostrapping

• In this example we'll use the ISLR::Portfolio data set.
  
• This data set contains the returns for two investment assets (X and Y).

• Here, our goal is going to be minimizing the risk of investing a fixed sum of money in each asset.
  
• Mathematically, we can achieve this by minimizing the variance of our investment using the statistic \[ \hat\alpha = \frac{\hat\sigma^2_Y - \hat\sigma_{XY}}{\hat\sigma^2_X +\hat\sigma^2_Y-2\hat\sigma_{XY}} \tag{5} \]
• Thus, we need to create a function that will compute this test statistic:

statistic <- function(data, index) {
  x <- data$X[index]
  y <- data$Y[index]
  (var(y) - cov(x, y)) / (var(x) + var(y) - 2* cov(x, y))
}

• Now we can compute \[\hat\alpha\] for a specified subset of our portfolio data:

portfolio <- ISLR::Portfolio
statistic(portfolio, 1:100)

## [1] 0.576

• Next, we can use sample to randomly select 100 observations from the range 1 to 100, with replacement.
• This is equivalent to constructing a new bootstrap data set and recomputing \[\hat\alpha\] based on the new data set.
  

statistic(portfolio, sample(100, 100, replace = TRUE))

## [1] 0.467

• If you re-ran this function several times you'll see that you are getting a different output each time.
  
• What we want to do is run this many times, record our output each time, and then compute a valid standard error of all the outputs.
• To do this we can use boot and supply it our original data, the function that computes the test statistic, and the number of bootstrap replicates (R).

set.seed(123)
boot(portfolio, statistic, R = 1000)

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = portfolio, statistic = statistic, R = 1000)
## 
## 
## Bootstrap Statistics :
##     original  bias    std. error
## t1*    0.576  0.0024      0.0875

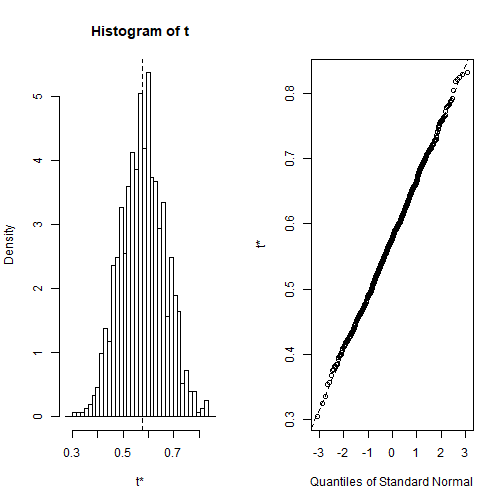
• The final output shows that using the original data, \[\hat\alpha = 0.5758\], and it also provides the bootstrap estimate of our standard error \[SE(\hat\alpha) = 0.0875\].
• Once we generate the bootstrap estimates we can also view the confidence intervals with boot.ci and plot our results:

## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = result, type = "basic")
## 
## Intervals : 
## Level      Basic         
## 95%   ( 0.396,  0.738 )  
## Calculations and Intervals on Original Scale

• We can use this same concept to assess the variability of the coefficient estimates and predictions from a statistical learning method such as linear regression.
• For instance, here we'll assess the variability of the estimates for \[\beta_0\] and \[\beta_1\], the intercept and slope terms for the linear regression model that uses horsepower to predict mpg in our auto data set.
  

• First, we create the function to compute the statistic of interest.
• We can apply this to our entire data set to get the baseline coefficients.

library(tidyverse)
auto <- as_tibble(ISLR::Auto)
statistic <- function(data, index) {
  lm.fit <- lm(mpg ~ horsepower, data = data, subset = index)
  coef(lm.fit)
}

statistic(auto, 1:392)

## (Intercept)  horsepower 
##      39.936      -0.158

set.seed(123)
boot(auto, statistic, 1000)

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = auto, statistic = statistic, R = 1000)
## 
## 
## Bootstrap Statistics :
##     original    bias    std. error
## t1*   39.936  0.029596      0.8635
## t2*   -0.158 -0.000294      0.0076

• This indicates that the bootstrap estimate for \(SE(\beta_0)\) is 0.86, and that the bootstrap estimate for \(SE(\beta_1)\) is 0.0076.
• If we compare these to the standard errors provided by the summary function we see a difference.
  

## 
## Call:
## lm(formula = mpg ~ horsepower, data = auto)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -13.571  -3.259  -0.344   2.763  16.924 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 39.93586    0.71750    55.7   <2e-16 ***
## horsepower  -0.15784    0.00645   -24.5   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.91 on 390 degrees of freedom
## Multiple R-squared:  0.606,  Adjusted R-squared:  0.605 
## F-statistic:  600 on 1 and 390 DF,  p-value: <2e-16

• This difference suggests the standard errors provided by summary may be biased.
• That is, certain assumptions may be violated which is causing the standard errors in the non-bootstrap approach to be different than those in the bootstrap approach.
• This may be due to the fact that this might be better modeled by a quadratic.

quad.statistic <- function(data, index) {
  lm.fit <- lm(mpg ~ poly(horsepower, 2), data = data, subset = index)
  coef(lm.fit)
}

set.seed(1)
boot(auto, quad.statistic, 1000)

## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = auto, statistic = quad.statistic, R = 1000)
## 
## 
## Bootstrap Statistics :
##     original  bias    std. error
## t1*     23.4 0.00394       0.226
## t2*   -120.1 0.11731       3.701
## t3*     44.1 0.04745       4.329

• Now if we compare the standard errors between the bootstrap approach and the non-bootstrap approach we see the standard errors align more closely.
  
• This better correspondence between the bootstrap estimates and the standard estimates suggest a better model fit.
  
• Thus, bootstrapping provides an additional method for assessing the adequacy of our model's fit.

## 
## Call:
## lm(formula = mpg ~ poly(horsepower, 2), data = auto)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -14.714  -2.594  -0.086   2.287  15.896 
## 
## Coefficients:
##                      Estimate Std. Error t value Pr(>|t|)    
## (Intercept)            23.446      0.221   106.1   <2e-16 ***
## poly(horsepower, 2)1 -120.138      4.374   -27.5   <2e-16 ***
## poly(horsepower, 2)2   44.090      4.374    10.1   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 4.37 on 389 degrees of freedom
## Multiple R-squared:  0.688,  Adjusted R-squared:  0.686 
## F-statistic:  428 on 2 and 389 DF,  p-value: <2e-16